三叶结

295672500

三叶结

方法一：

1.选用（柱面坐标系，即极坐标）曲线方程

theta=t*180

r=65*sin(3*theta)

2.在曲线平面进行草绘，参照三叶曲线进行偏移45

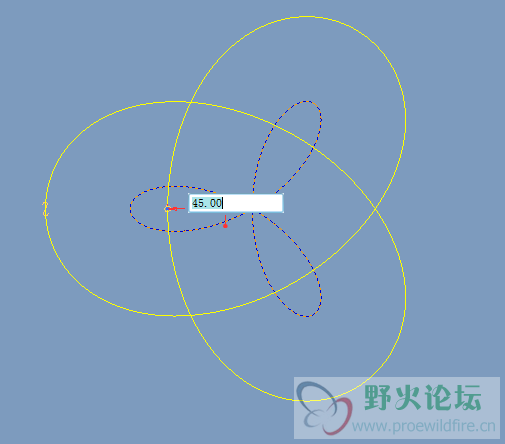
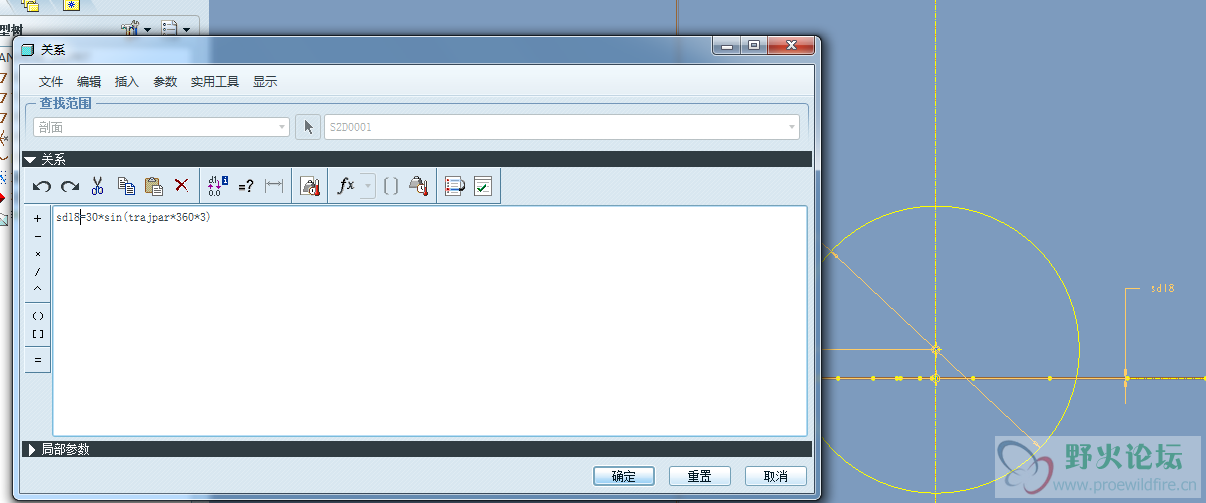
3.使用可变截面扫描，利用草绘曲线为扫引轨迹，圆心高低位置由公式驱动sd18=30*sin(trajpar*360*3)

4.最终结果

方法二：
使用参数方程进行调整

x=Asint+Bsin2t

y=Ccost+Dcos2t

z=Esin3t

其中参数A～E影响三叶结各环的宽度、间距等，使用不同参数得到的模型，其形状、本质也有所不同，如图所示:

效果最佳为：A=C=1,B=2,D=-2,E=-1

三叶结的三维建模

1.扫描轨迹的参数方程

    在笛卡尔坐标系下，通过曲线方程建立曲线扫描轨迹，模型大小要适中，故三叶结轨迹曲线参数方程如下所示：

   x=20×sin（t×360）+40×sin（2×t×360）

   y=20×cos（t×360）-40×cos（2×t×360）

   z=-20×sin（3×t×360）

   此时，曲线所在区域为100mm×100mm×60mm的一个立方体空间，得到轨迹曲线如图

2.使用“可变截面扫描”，通过起始点并且垂直于扫描轨迹的平面作为绘制扫描截面的草绘平面，绘制直径为20mm的扫掠截面，如图

3.最终结果

三叶结的方程

  在纽结理论中，三叶结（trefoil knot）是一种最简单的非平凡纽结。可以用反手结连接两个末端而达成。它是唯一一种有3个交叉的纽结。它也可以描述为环面纽结。由于三叶结的结构极为简单，它是研究纽结理论很重要的基本案例，在拓扑学、几何学、物理学、化学领域，有广泛的用途。

1.三叶结可以由以下的参数方程确定：

  x=sin(t)+2sin(t)

  y=cos(t)-2cos(2t)

  z=-sin3(t)

2.三叶结也可以看作环面纽结。对应的参数方程为：

   x=(2+cos3t)cos2t

   y=(2+cos3t)sin2t

   z=sin3t

3. 三叶结平面极坐标方程

  ρ(θ)=cos(3θ)

                                    三叶结左、右旋

1.左旋方程

x=20*sin(t*360)+40*sin(2*t*360)

y=20*cos(t*360)-40*cos(2*t*360)

z=-20*sin(3*t*360)

结果

2.右旋方程

x=20*sin(t*360)+40*sin(2*t*360)

y=20*cos(t*360)-40*cos(2*t*360)

z=20*sin(3*t*360)

平面极坐标方程推广

ρ(θ)=cos(nθ)

     

     

                                       

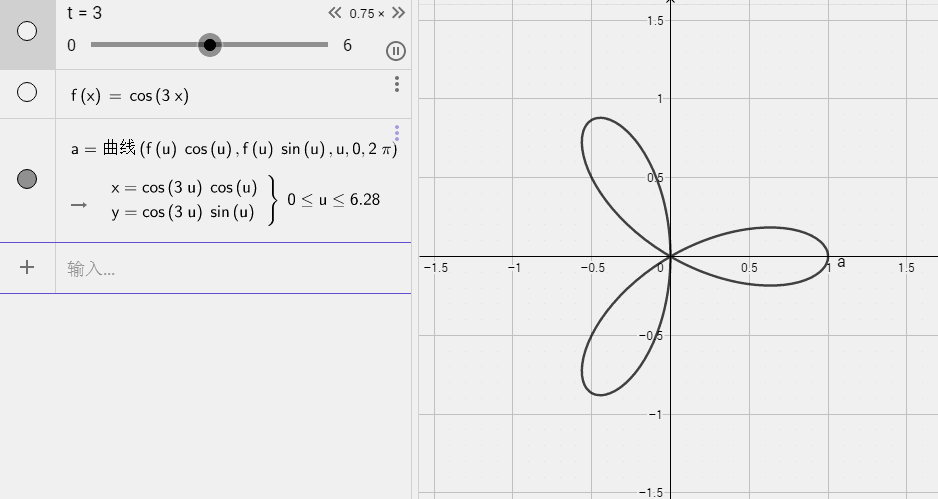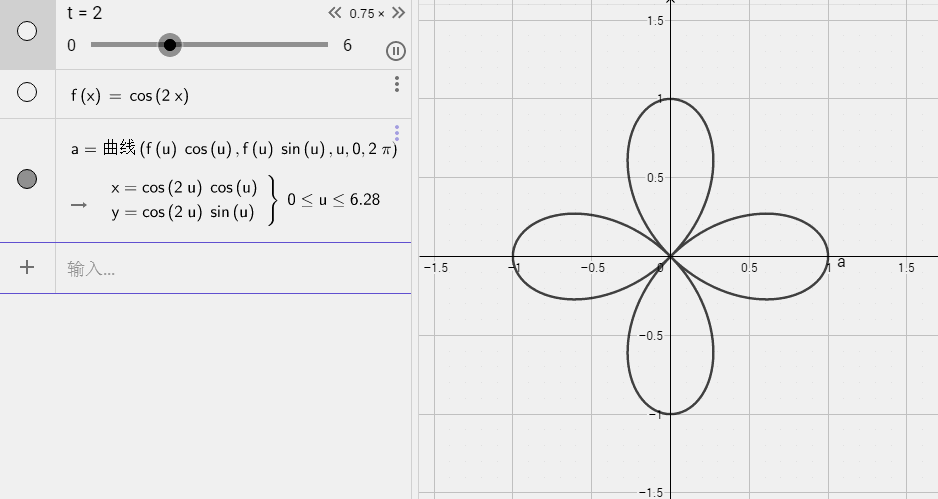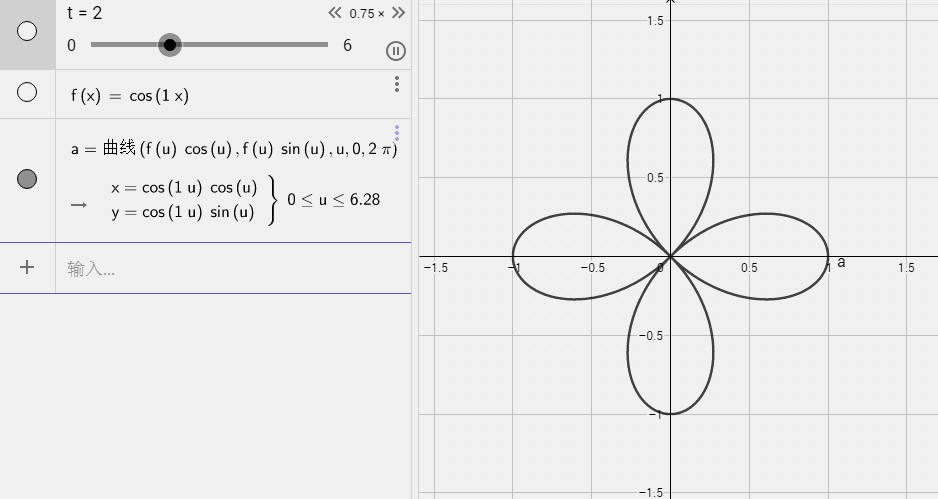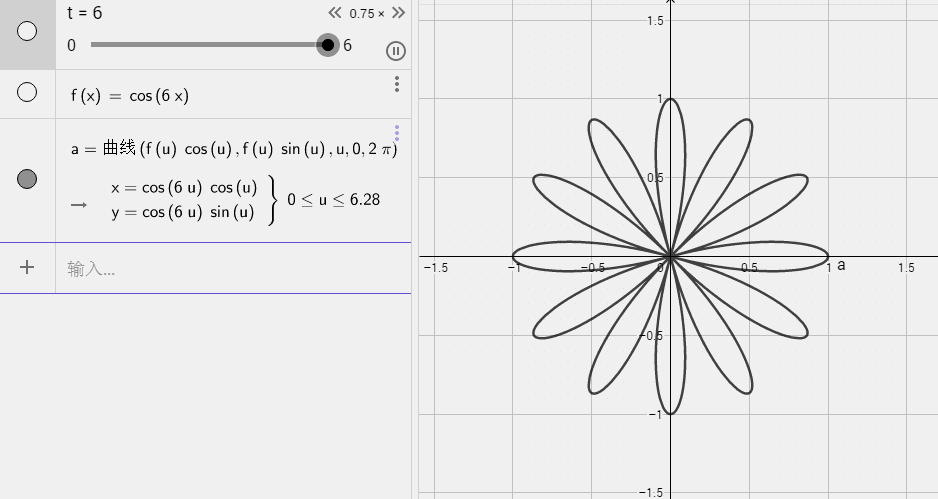
五叶结

七叶结

野火

谢谢朋友分享

JUN565764045

谢谢分享。

zzcc-apple

楼主数学好厉害。

sdgdjgb

Mathcad软件？

sdgdjgb

295672500

sdgdjgb 发表于 2018-3-23 21:11
Mathcad软件？

mathCAD  和  geogebra

295672500

sanyejie_01.prt.rar (421.45 KB, 下载次数: 16)

2018-3-23 21:54 上传

点击文件名下载附件
proe5.0

sanyejie_02.prt.rar (372.31 KB, 下载次数: 17)

2018-3-23 21:54 上传

点击文件名下载附件
proe5.0

chenyu1219

谢谢分享！

futurism

感谢分享！